By Nina Engelhardt
1. Contrast
Mentioning ‘literature and mathematics’ in one breath often leads to raised eyebrows and reminders of the stereotypical contrast between the fields: the rigour and exactitude of mathematics and its universal truths can be seen as diametrically opposed to literature and its focus on the particular, the subjective, and the changing conditions of human life. And while reading literary fiction is widely enjoyed, many perceive mathematics as arcane and forbidding. Yet, as the next points show, both literary writers and mathematicians have also explored similarities and connections between their fields.
2. Connection
Various texts written in and about the early twentieth century suggest connections between mathematics and other fields, not least literature, and propose that maths functions as a model of modern times. Hermann Broch’s novel trilogy The Sleepwalkers (1930–32) pronounces ‘research into first principles of modern mathematics’ as ‘the clearest example’ of a ‘sweeping revolution in the style of thinking’. Robert Musil’s The Man without Qualities (1930/32) establishes maths as ‘the new method of thought itself, the mind itself, the very wellspring of the times’. Thomas Pynchon’s Against the Day (2006) similarly suggests viewing the period in terms of a connection to maths: ‘The political crisis in Europe maps into the crisis in mathematics’. And while an equation in Pynchon’s Gravity’s Rainbow (1973) presents maths in all its fascinating and intimidating complexity:
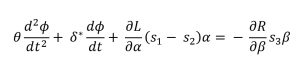the formula also functions as a symbol of the control that a small privileged group exercises over the life paths of the powerless majority. For more information, click here.
3. Crisis
The early twentieth century can be understood as a period of vanishing certainties: Christian faith is on the wane, the First World War puts into question belief in progress and humanity, the rise of movements towards gender equality and workers’ rights initiate changes in social structures, and traditional forms and techniques in literature seem inadequate to represent a drastically changed reality. Less well remembered is the so-called ‘foundational crisis of mathematics’ that disconcerted mathematicians, philosophers, and literary writers as well as the public: it marks a period of attempting – and failing – to set maths on stable foundations. As paradoxes continued to thwart these efforts, concern about the consequences grew: ‘If mathematical thinking is defective, where are we to find truth and certitude?’, David Hilbert, the probably most famous mathematician of the time, asked.
4. Language
Is mathematics a language? Maybe even a ‘perfect’ language? The dream of an unambiguous means of communication manifests in a large number of artificial languages in the decades around 1900. Gottlob Frege suggested logic as the basis of both maths and language, and developed an ideal language based on the model of mathematics and its definite rules. When early-twentieth-century literature experienced a ‘crisis of language’ around 1900, writers turned to mathematics to retrieve some of the clarity and certainty they felt to have been lost in everyday and literary communication.
5. Freedom
If mathematics is understood as a language, the question of its relation to the world arises. Do words and mathematical terms directly refer to reality? Where linguist Ferdinand de Saussure argued that language has to be considered as a system of signs that does not take account of the outward referent, mathematics underwent a similar self-referential turn: it came to be understood to have no direct relation to physical reality. The term and concept of imaginary numbers proved particularly fruitful for literary writers to explore this idea and its implications for their own field. That maths develops free from the ties of referentiality inspired writers to claim a similar freedom from reality in their fiction: liberating themselves from realism’s aims for representation, modernist writers draw connections with maths to emphasise the internal logic of self-contained worlds and the creative possibilities this implies.
6. Form
‘The essence of mathematics is its freedom’, so the founder of the formalist school of maths, Georg Cantor, put it. Formalism works from the assumption that maths ‘is’ its language – anything that can be formulated in mathematical language without contradicting the rules of the system exists: for example, it is sufficient that imaginary numbers can be formulated in the system of complex numbers – there is no need for a relation to nature or intuitive grasp of these numbers to ensure their validity. In this sense, the freedom of maths relies on its definition as pure form. As early twentieth-century literature also increasingly focused on formal features, various writers turned to maths as the perfect example for the possibilities of formal innovation.
7. Intuition
Where the formalist school sees maths as a freely developing language, the Dutch mathematician E.L.J. Brouwer aimed to liberate maths from language, which he saw as an instrument of conflict that creates misunderstandings and was partly responsible for the First World War. In his view, maths originates outside of language, as a thought-construct in human intuition. Literature in the early twentieth century also explores realms outside reason – such as madness, trance, and dream – and writers also draw on maths to explore and legitimate the role of intuition in life and literature.
8. Fiction
Modern mathematics, seen as a realm apart from reality and freely developing new possibilities by formal description, shares some characteristics with literary fiction. Writers such as Pynchon, Broch, and Musil explore this idea and compare formal mathematical creations with the possibilities of literature where description can build fictional worlds. Also examining the notion that maths makes use of ‘fictions’, for example in the suggestively named concept of imaginary numbers, these writers draw on maths to develop new ideas of literary fiction and its relations to reason and reality.
9. Modernism
When, as introduced above, modern mathematics questions its relation to the world, becomes self-referential, experiences a sense of crisis and a focus on form, it exhibits characteristics commonly associated with modernist literature and art. Historians of maths have therefore introduced the notion of a ‘mathematical modernism’. Examining literary texts such as those by Pynchon, Broch, and Musil can advance this idea: by interrelating mathematical and literary developments, they point to characteristics shared between these fields and thus support the idea that maths does not only become modern but modernist, that is, that apart from undergoing a process of modernisation, maths is part of modernist culture.
10. Fascination
Last and foremost: when working on literature and mathematics, we can count on being fascinated – by the history of maths, how literary works engage with it, and, most of all, by the way questions and concerns appear in both fields and mirror and enhance each other.
Nina Engelhardt is a lecturer in English and American Literature at the University of Cologne. She received her PhD from the University of Edinburgh and has since held research and teaching positions at the University of Edinburgh, the Institute for Advanced Studies in the Humanities, Edinburgh, and the Research Group ‘Transformations’ at the University of Cologne. Her book Modernism, Fiction and Mathematics published in June 2018.
